Interpreter Design Pattern – Design to Implementation
Implementing the Interpreter Design Pattern based upon a Design.

Introduction
This blog continues the Interpreter Design Pattern series by expanding upon the Interpreter Implementation progresses from the Design that was constructed for Rational Expression Evaluator Use Case Interpreter in the use case example.
This gets a bit long, but it’s all implementation. There is no theory, and there was much rejoicing.
The Rational Expression Evaluator Use Case Class Diagram
Here’s a copy of the UML class diagram from Grammar to Design Blog. It follows the same dependency management principles presented in Hexagonal Architecture – Why it works. These principles apply to design in general, and not just to Hexagonal Architectures.
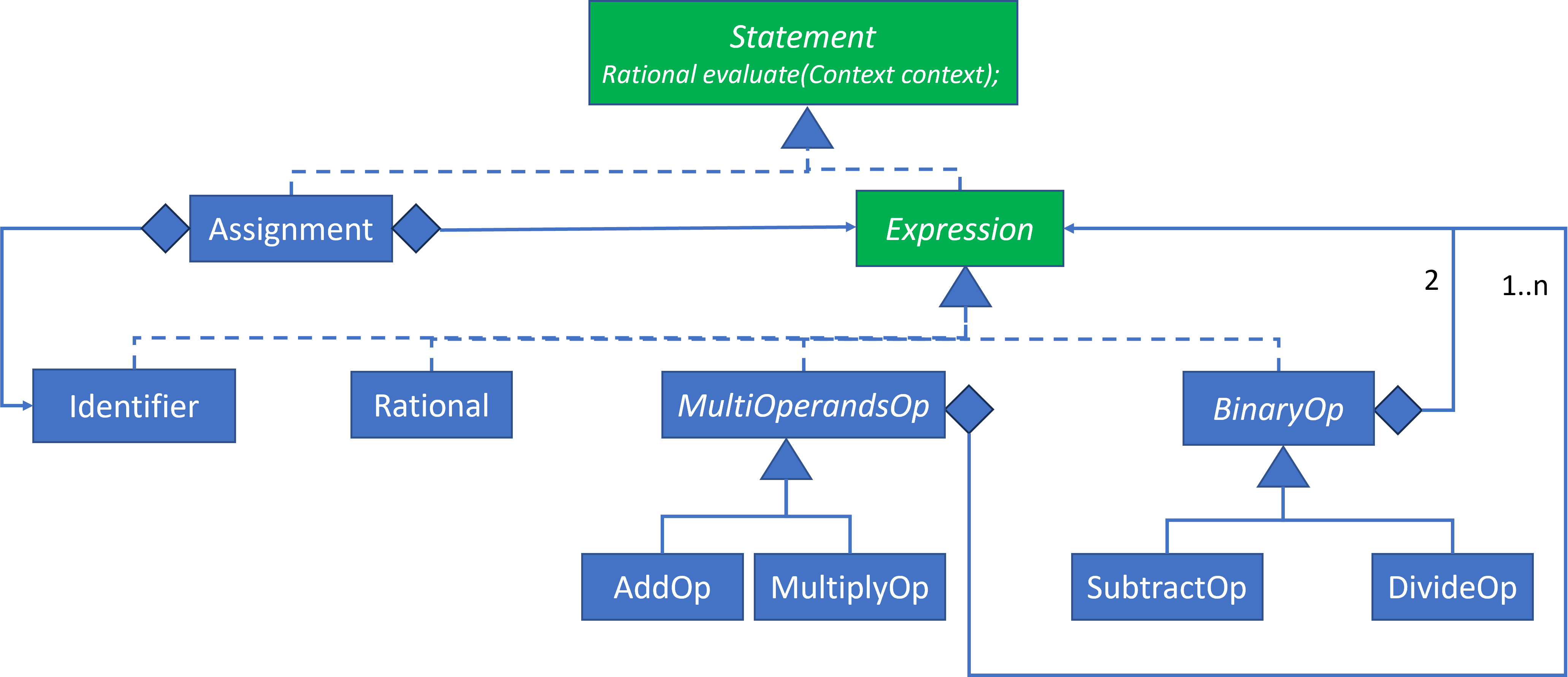
This design has no external dependencies. Therefore, it will not require Test Doubles to test it. When there are dependencies, we’ll be using actual elements, such as Rational.
Where to start?
While we can technically start implementation anywhere, I tend to like to use dependency management principles, listed above, as a guideline. I start with the elements with the least number of dependencies in the design, which is the Statement above. It’s an interface with only a declaration, so there’s nothing needed other than to declare it.
The next least dependent element is Expression, which is also an interface, but without any methods. Its implementation is even simpiler.
Looking at the classes that implement Expression, I’m going to choose to implement Rational first, because:
- It’s in the
Statementmethod definition, so I’m going to need it anyway. - I suspect that
Rationalwill require the most implementation effort, so let’s get it done first.
Since Rational depends upon Expression, which depends upon Statement, let’s focus upon this subset of the design:
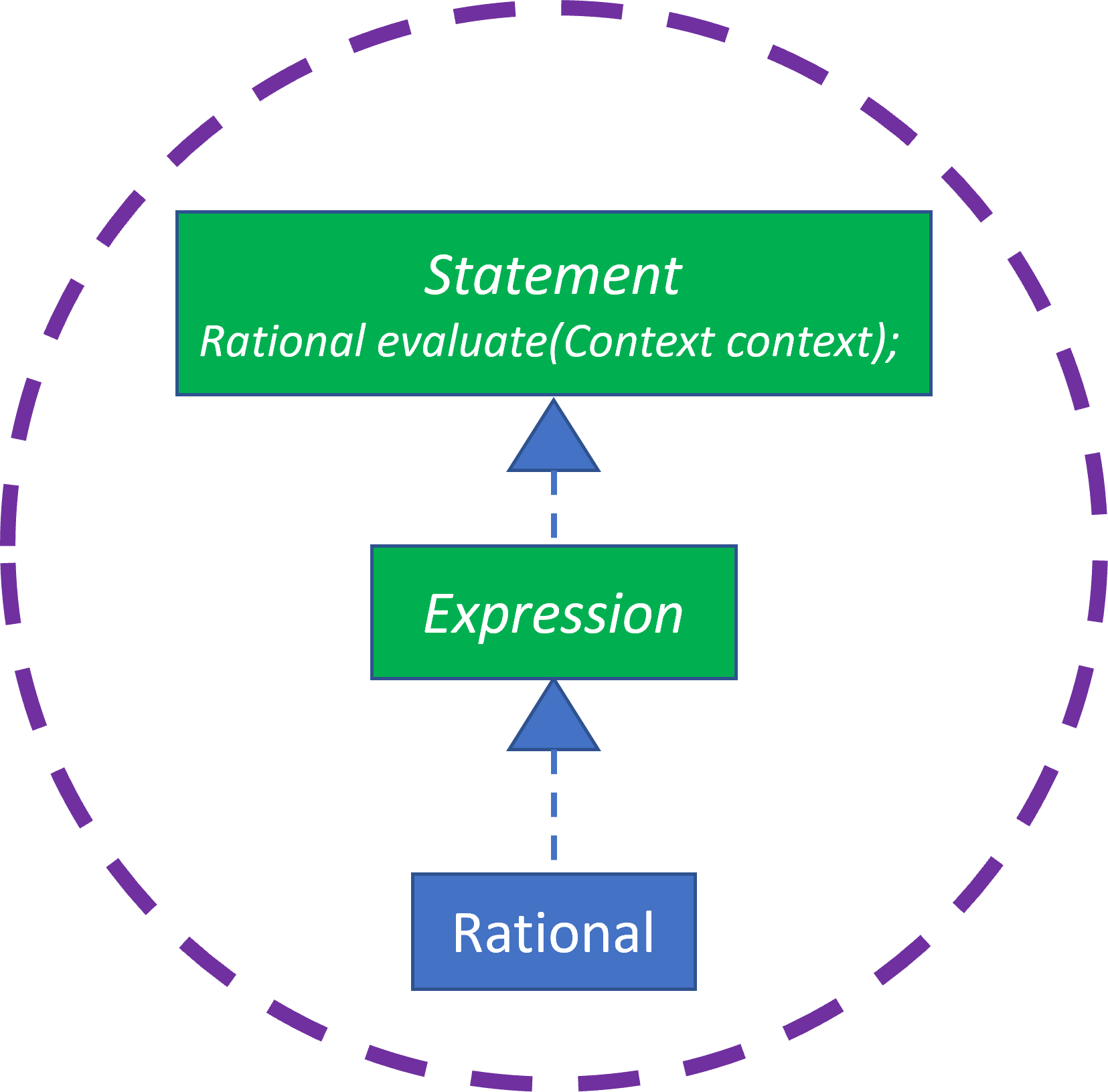
Bare Bones Implementation and Test Environment
My implementation will be in Java. I’m going to include everything from soup to nuts in one file, so anyone can copy-and-paste it. I’m going to use my own test harness, so that there are no environmental dependencies.
Here is my first complete program that confirms the first test of the first Rational behavior. I’ll provide code snippets as I progress and the entire Java code at the end of this blog.
import java.util.*;
public class RationalEvaluator {
public static void main(String[] args) throws Exception {
Test.test();
}
}
interface Statement {
Rational evaluate(Context context);
}
class Context {}
interface Expression extends Statement {}
class Rational implements Expression {
public Rational(String rationalString) {}
public Rational evaluate(Context context) {
return this;
}
@ Override
public String toString() {
return "0";
}
}
class Test {
public static void test() throws Exception {
testDesign();
System.out.println("TESTS PASS");
}
private static void testDesign() throws Exception {
assertEquals("0", new Rational("0").evaluate(null).toString());
}
private static void assertEquals(String expected, String actual) throws Exception {
if (!expected.equals(actual)) {
System.out.format("expected=%s, actual=%s\n", expected, actual);
throw new Exception();
}
}
}
Rational Test and Implementation
I will layer in Rational behaviors using Test-Driven Development techniques. I will introduce failing tests first and then update the implementation so that they all pass.
NOTE: I will not be testing all edge cases for two reasons:
- The parser should only return valid Strings.
- I want to keep the implementation as tight as possible. If this were for production, then I’d probably do more validation checking.
Implement Rationals Supporting Integers
We want Rationals to support Integers.
I can inject null for the Context, since Rational doesn’t reference it. If it did, then the test would throw a NullPointerException and I’d know that I would need to provide an object.
Test:
assertEquals("0", new Rational("0").evaluate(null).toString());
assertEquals("1", new Rational("1").evaluate(null).toString());
assertEquals("-1", new Rational("-1").evaluate(null).toString());
assertEquals("5", new Rational(" 5 ").evaluate(null).toString());
assertEquals("5", new Rational(" 5 ").evaluate(null).toString());
The previous hardcoded Rational returning “0” no longer passes the new unit tests. I updated Rational as:
class Rational implements Expression {
private final int rational;
public Rational(String rationalString) {
rational = Integer.parseInt(rationalString);
}
public Rational evaluate(Context context) {
return this;
}
@ Override
public String toString() {
return String.valueOf(rational);
}
}
Implement Rationals Supporting Fractions
We want Rationals to support fractions.
Test:
assertEquals("1/2", new Rational(" 1/2 ").evaluate(null).toString());
assertEquals("-1/2", new Rational(" -1/2 ").evaluate(null).toString());
assertEquals("2/3", new Rational("2 / 3").evaluate(null).toString());
assertEquals("2/3", new Rational(" 2 / 3 ").evaluate(null).toString());
Implementation:
class Rational implements Expression {
private final int numerator;
private final int denominator;
public Rational(String rationalString) {
if (!rationalString.contains("/")) {
numerator = Integer.parseInt(rationalString.trim());
denominator = 1;
} else {
String[] integers = rationalString.split("/");
numerator = Integer.parseInt(integers[0].trim());
denominator = Integer.parseInt(integers[1].trim());
}
}
public Rational evaluate(Context context) {
return this;
}
@ Override
public String toString() {
if (denominator == 1) {
return String.valueOf(numerator);
}
return String.valueOf(numerator) + "/" + String.valueOf(denominator);
}
}
Implement Rationals in their Most Reduced Form
We want Rationals in their reduced form.
Test:
assertEquals("1/2", new Rational("2/4").evaluate(null).toString());
assertEquals("1/2", new Rational("32/64").evaluate(null).toString());
assertEquals("1/4", new Rational("30 / 120").evaluate(null).toString());
Implementation:
class Rational implements Expression {
private final int numerator;
private final int denominator;
public Rational(String rationalString) {
int numerator;
int denominator;
if (!rationalString.contains("/")) {
numerator = Integer.parseInt(rationalString.trim());
denominator = 1;
} else {
String[] integers = rationalString.split("/");
numerator = Integer.parseInt(integers[0].trim());
denominator = Integer.parseInt(integers[1].trim());
}
int divisor = denominator;
while (divisor > 1) {
if (numerator % divisor == 0 && denominator % divisor == 0) {
numerator = numerator / divisor;
denominator = denominator / divisor;
} else {
divisor--;
}
}
this.numerator = numerator;
this.denominator = denominator;
}
public Rational evaluate(Context context) {
return this;
}
@ Override
public String toString() {
if (denominator == 1) {
return String.valueOf(numerator);
}
return String.valueOf(numerator) + "/" + String.valueOf(denominator);
}
}
Implement Rationals Supporting Improper Fractions
We want Rationals to support improper fractions.
Test:
assertEquals("1 2/5", new Rational("7/5").evaluate(null).toString());
assertEquals("2 1/4", new Rational("36/16").evaluate(null).toString());
assertEquals("-2 1/4", new Rational("-36/16").evaluate(null).toString());
assertEquals("5", new Rational("15 / 3").evaluate(null).toString());
assertEquals("-3", new Rational("-15 / 5").evaluate(null).toString());
Implementation:
public String toString() {
if (denominator == 1) {
return String.valueOf(numerator);
} else if (Math.abs(numerator) > denominator) {
return String.format("%d %d/%d", numerator/denominator, Math.abs(numerator%denominator), denominator);
}
return String.valueOf(numerator) + "/" + String.valueOf(denominator);
}
Implement Rationals Supporting Improper Fractions
We want Rationals to support mixed & improper fractions.
Test:
assertEquals("1 5/6", new Rational("1 5/6").evaluate(null).toString());
assertEquals("2 2/3", new Rational(" 2 4 / 6 ").evaluate(null).toString());
assertEquals("4 1/2", new Rational(" 2 10 / 4 ").evaluate(null).toString());
assertEquals("5", new Rational(" 3 4 / 2 ").evaluate(null).toString());
Implementation:
public Rational(String rationalString) {
int integer = 0;
int numerator;
int denominator;
if (!rationalString.contains("/")) {
numerator = Integer.parseInt(rationalString.trim());
denominator = 1;
} else {
String[] integers = rationalString.split("/");
if (integers[0].trim().contains(" ")) {
String[] tokens = integers[0].trim().split("\\s+");
integer = Integer.parseInt(tokens[0].trim());
numerator = Integer.parseInt(tokens[1].trim());
} else {
numerator = Integer.parseInt(integers[0].trim());
}
denominator = Integer.parseInt(integers[1].trim());
numerator += integer * denominator ;
}
int divisor = denominator;
while (divisor > 1) {
if (numerator % divisor == 0 && denominator % divisor == 0) {
numerator = numerator / divisor;
denominator = denominator / divisor;
} else {
divisor--;
}
}
this.numerator = numerator;
this.denominator = denominator;
}
Implement Rationals as Value Objects
Rational is a value object. It is immutable. Its field attributes are final and cannot be modified once set in its constructor. All fraction normalization, i.e., reduced form, improper fractions and mixed fractions, resides in the constructor. Rationals will always be constructed in normalized form and can never be modified subsequently.
This means that in all other arithmetic operations, we don’t need to worry about all of these normalization forms. We can create a Rational string with any integer numerator and denominator values that are created in fractional arithmetic, and Rational will do all of the normalization for us automatically.
BinaryOp, SubtractOp and DivideOp Test and Implementation
With Rational done, I can go just about anywhere. I’m going to start with BinaryOp. This expands the scope of the implementation to:
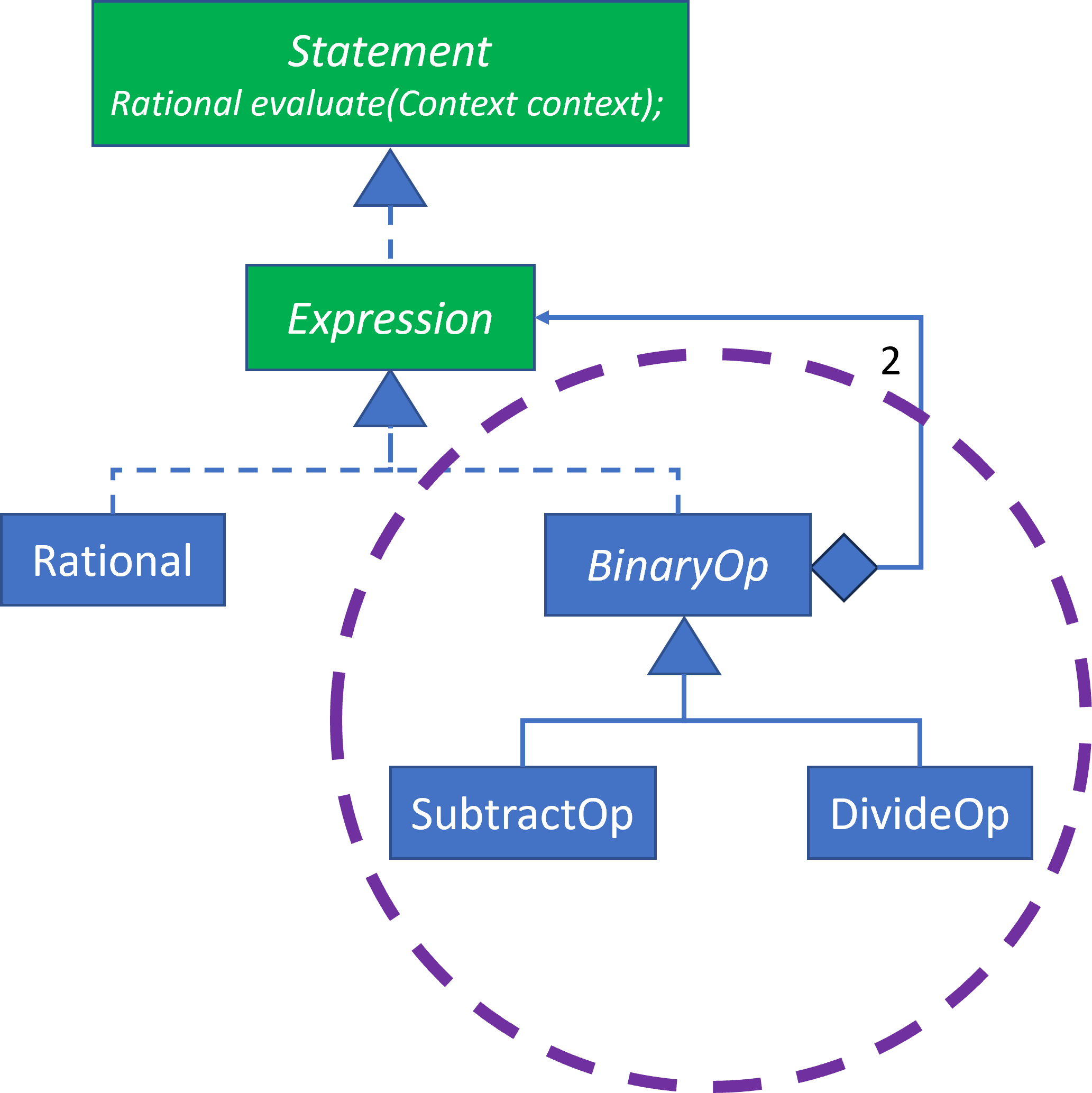
These classes involve fractional arithmetic, so you might need to brush up a bit on that.
SubtractOp is a BinaryOp
I anticipate BinaryOp using the Template Design Pattern. I would usually test and implement a Template Method design in isolation using test double as the concrete class. But since the concrete classes are so well defined, I’m going to test and implement the SubstractOp and BinaryOp together.
The tests confirm that SubtractOp will subtract one Rational from another Rational returning its Rational difference. I don’t need to worry about Rational argument formatting with spaces, since the previous tests confirm that.
Test:
assertEquals("1", new SubtractOp(new Rational("4"), new Rational("3")).evaluate(null).toString());
assertEquals("2 1/2", new SubtractOp(new Rational("4"), new Rational("1 1/2")).evaluate(null).toString());
assertEquals("-3", new SubtractOp(new Rational("2"), new Rational("5")).evaluate(null).toString());
I will need to easily extract the numerator and denominator from Rational, so I’ve added the following accessor methods to Rational:
public int getNumerator() {
return numerator;
}
public int getDenominator() {
return denominator;
}
Here is my first draft for BinaryOp and SubtractOp, but I suspect I might refactor them once I implement DivideOp.
abstract class BinaryOp implements Expression {
private final Expression operand1;
private final Expression operand2;
public BinaryOp(Expression operand1, Expression operand2) {
this.operand1 = operand1;
this.operand2 = operand2;
}
public Rational evaluate(Context context) {
return operation(operand1, operand2, context);
}
abstract protected Rational operation(Expression operand1, Expression operand2, Context context);
}
class SubtractOp extends BinaryOp {
public SubtractOp(Expression op1, Expression op2) {
super(op1, op2);
}
protected Rational operation(Expression operand1, Expression operand2, Context context) {
Rational rational1 = operand1.evaluate(context);
Rational rational2 = operand2.evaluate(context);
int rational1Numerator = rational1.getNumerator();
int rational1Denominator = rational1.getDenominator();
int rational2Numerator = rational2.getNumerator();
int rational2Denominator = rational2.getDenominator();
int numerator = rational1Numerator * rational2Denominator - rational2Numerator * rational1Denominator;
int denominator = rational1Denominator * rational2Denominator;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
DivideOp is a BinaryOp
DivideOp is a BinaryOp as well, but since BinaryOp has already been implemented, I only need to test and implement DivideOps.
Test:
assertEquals("2", new DivideOp(new Rational("4"), new Rational("2")).evaluate(null).toString());
assertEquals("3/4", new DivideOp(new Rational("3"), new Rational("4")).evaluate(null).toString());
assertEquals("1", new DivideOp(new Rational("3"), new Rational("3")).evaluate(null).toString());
assertEquals("57/110", new DivideOp(new Rational("3 4/5"), new Rational("7 1/3")).evaluate(null).toString());
Implementation:
class DivideOp extends BinaryOp {
public DivideOp(Expression op1, Expression op2) {
super(op1, op2);
}
protected Rational operation(Expression operand1, Expression operand2, Context context) {
Rational rational1 = operand1.evaluate(context);
Rational rational2 = operand2.evaluate(context);
int rational1Numerator = rational1.getNumerator();
int rational1Denominator = rational1.getDenominator();
int rational2Numerator = rational2.getNumerator();
int rational2Denominator = rational2.getDenominator();
int numerator = rational1Numerator * rational2Denominator;
int denominator = rational1Denominator * rational2Numerator;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
Refactoring SubtractOp, DivideOp and BinaryOp
The first version has duplication that I’d like to refactor. There’s code in the concrete classes, which I think can be moved into BinaryOp. I don’t need to change the tests, only the implementation:
abstract class BinaryOp implements Expression {
private final Expression operand1;
private final Expression operand2;
public BinaryOp(Expression operand1, Expression operand2) {
this.operand1 = operand1;
this.operand2 = operand2;
}
public Rational evaluate(Context context) {
Rational rational1 = operand1.evaluate(context);
Rational rational2 = operand2.evaluate(context);
return operation(rational1.getNumerator(), rational1.getDenominator(), rational2.getNumerator(), rational2.getDenominator());
}
abstract protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2);
}
class SubtractOp extends BinaryOp {
public SubtractOp(Expression op1, Expression op2) {
super(op1, op2);
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * denominator2 - numerator2 * denominator1;
int denominator = denominator1 * denominator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
class DivideOp extends BinaryOp {
public DivideOp(Expression op1, Expression op2) {
super(op1, op2);
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * denominator2;
int denominator = denominator1 * numerator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
MultiOperandsOps, AddOp and MultiplyOp Test and Implementation
Next, I’ll add in the MultiOperandsOp, AddOp and MultiplyOp classes. These classes involve fractional arithmetic, so you might need to brush up a bit on that.
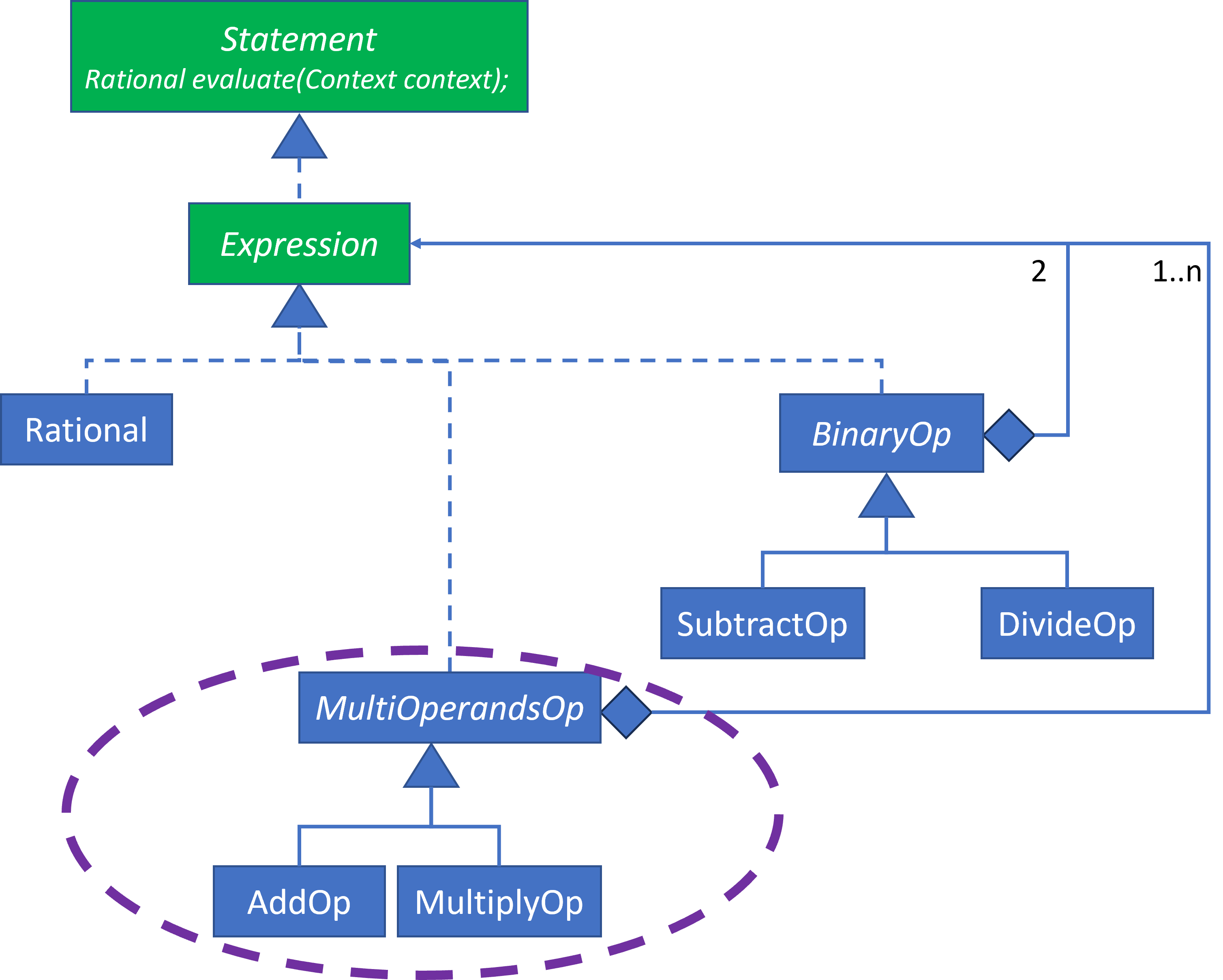
Notice that except for adding the two new accessors to Rational, nothing else has changed when implementing these classes.
Since MultiOperandsOp, et al., will look very similar to BinaryOp, et al., I’ll only provide the final version of the code. The only major distinction between these two sets of classes is that BinaryOp has two operands and MultiOperandsOp has any number of operands.
Test:
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("4"));
addOp.addExpression(new Rational("3"));
assertEquals("7", addOp.evaluate(null).toString());
}
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("1/2"));
addOp.addExpression(new Rational("1/6"));
assertEquals("2/3", addOp.evaluate(null).toString());
}
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("1/2"));
addOp.addExpression(new Rational("1/6"));
addOp.addExpression(new Rational("1/6"));
assertEquals("5/6", addOp.evaluate(null).toString());
}
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("1 1/2"));
addOp.addExpression(new Rational("2 1/6"));
addOp.addExpression(new Rational("3 1/6"));
addOp.addExpression(new Rational("4 1/6"));
assertEquals("11", addOp.evaluate(null).toString());
}
{
MultiOperandsOp multiplyOp = new MultiplyOp();
multiplyOp.addExpression(new Rational("4"));
multiplyOp.addExpression(new Rational("3"));
assertEquals("12", multiplyOp.evaluate(null).toString());
}
{
MultiOperandsOp multiplyOp = new MultiplyOp();
multiplyOp.addExpression(new Rational("4 1/2"));
multiplyOp.addExpression(new Rational("3 1/3"));
multiplyOp.addExpression(new Rational("2 1/6"));
assertEquals("32 1/2", multiplyOp.evaluate(null).toString());
}
Implementation:
abstract class MultiOperandsOp implements Expression {
private final List<Expression> expressions = new LinkedList<>();
public void addExpression(Expression expression) {
expressions.add(expression);
}
public Rational evaluate(Context context) {
Rational accumulator = getIdentity();
for(Expression expression : expressions) {
Rational operand = expression.evaluate(context);
accumulator = operation(accumulator.getNumerator(), accumulator.getDenominator(), operand.getNumerator(), operand.getDenominator());
}
return accumulator;
}
abstract protected Rational getIdentity();
abstract protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2);
}
class AddOp extends MultiOperandsOp {
protected Rational getIdentity() {
return new Rational("0");
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * denominator2 + numerator2 * denominator1;
int denominator = denominator1 * denominator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
class MultiplyOp extends MultiOperandsOp {
protected Rational getIdentity() {
return new Rational("1");
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * numerator2;
int denominator = denominator1 * denominator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
Identifier Test and Implementation
We’re done with arithmetic. Hurray! Now we can move to state, and Context is finally going to become a contributor. Up to this point, I’ve injected null for the Context without an issue since none of the previous classes use it.
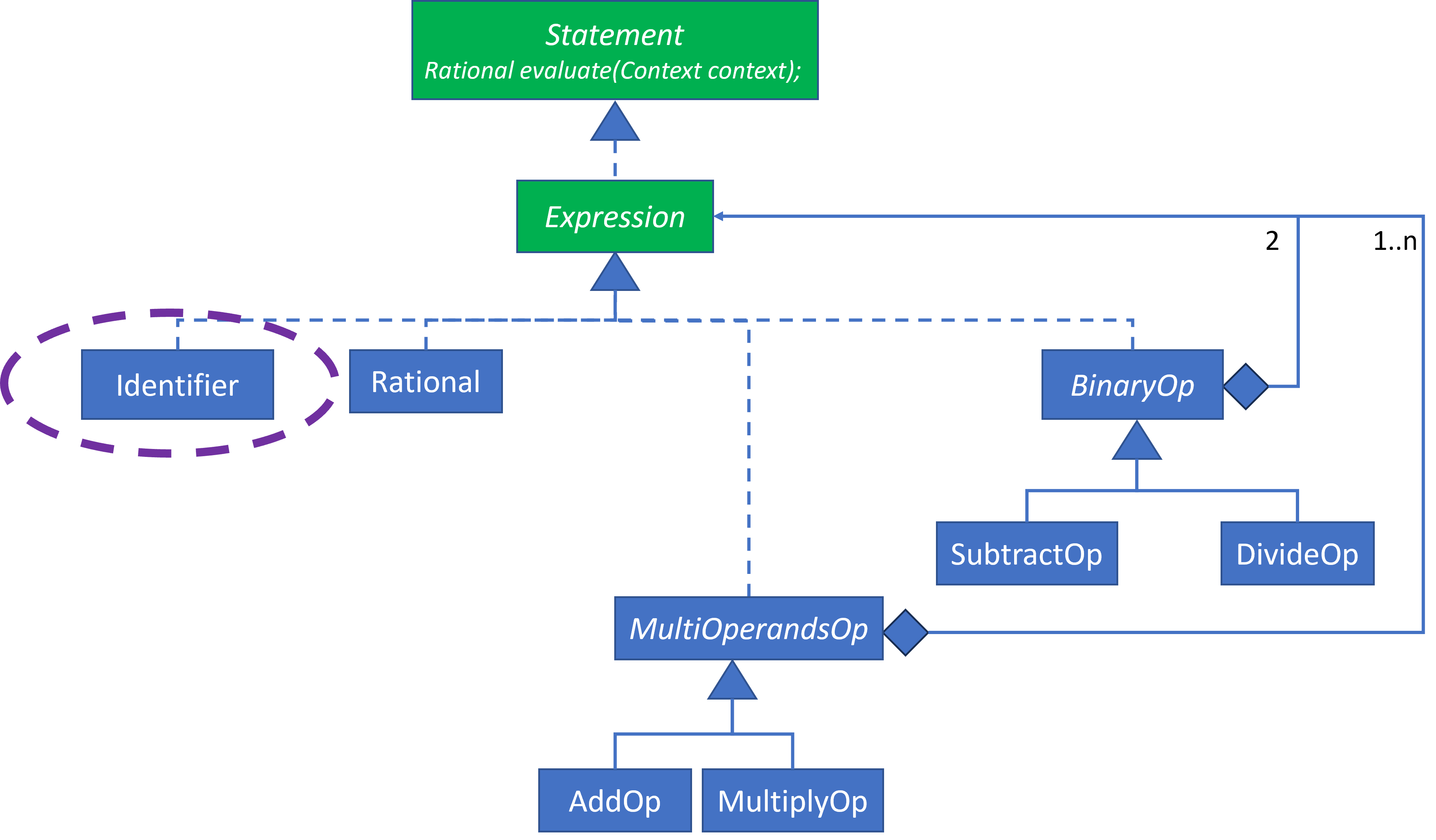
The Identifier implementation will extract a Rational from the Context based upon an identifier name. This will involve implementations for Context and Identifier.
Test:
{
Context context = new Context();
assertEquals("0", new Identifier("a").evaluate(context).toString()); // Evaluates to zero when not found.
context.add("a", new Rational("5"));
assertEquals("5", new Identifier("a").evaluate(context).toString());
context.add("a", new Rational("7"));
assertEquals("7", new Identifier("a").evaluate(context).toString());
}
Implementation:
class Context {
private final Map<String, Rational> state = new HashMap<>();
public void add(String identifier, Rational rational) {
state.put(identifier, rational);
}
public boolean containsKey(String identifier) {
return state.containsKey(identifier);
}
public Rational getRational(String identifier) {
return state.get(identifier);
}
}
class Identifier implements Expression {
private final String identifier;
public Identifier(String identifier) {
this.identifier = identifier;
}
public Rational evaluate(Context context) {
if (!context.containsKey(identifier)) return new Rational("0");
return context.getRational(identifier);
}
}
Assignment Test and Implementation
We’re in the homestretch. The Assignment class is the last one to be implemented.
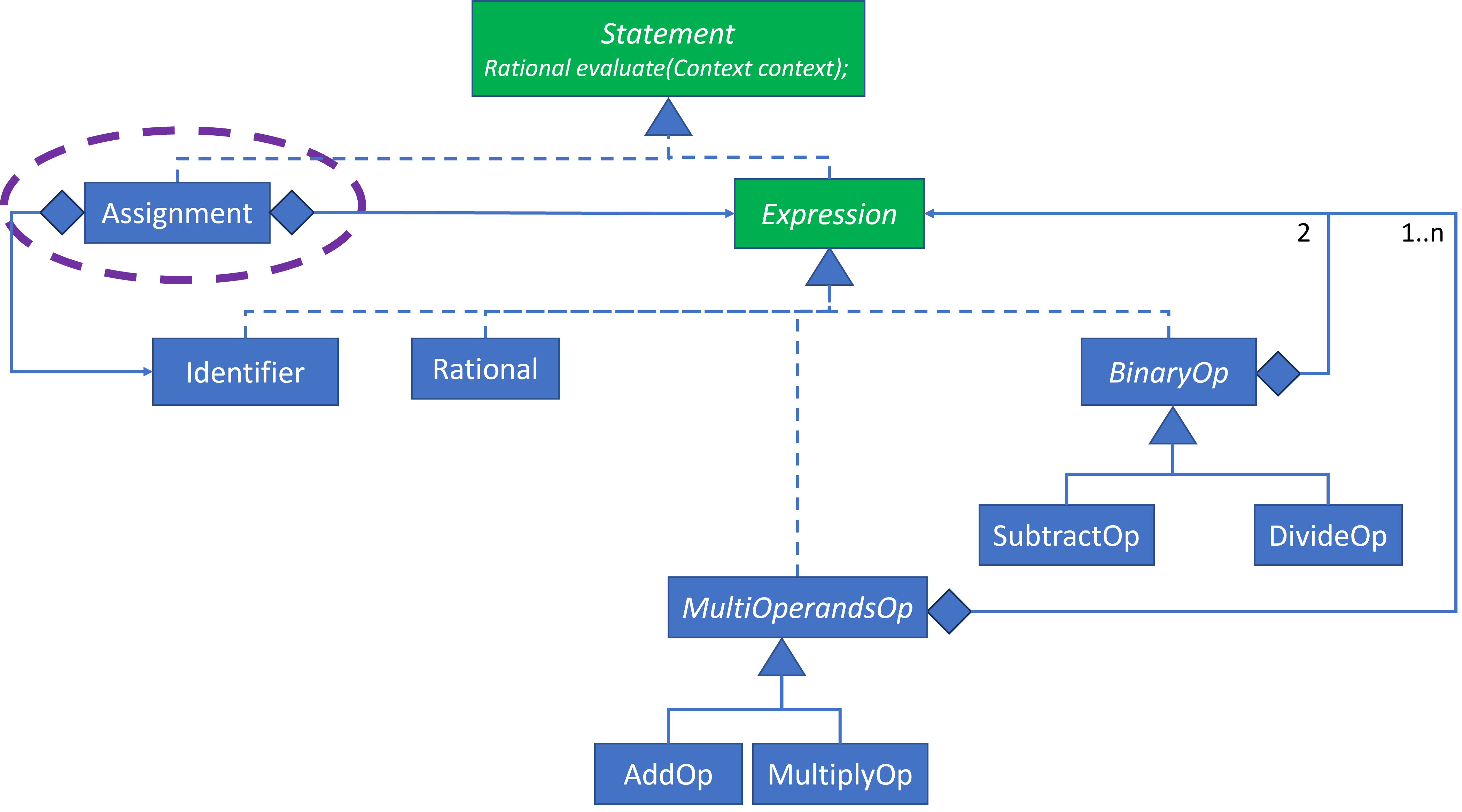
This should be about as straightforward as Identifier. While the design indicates a dependency upon Identifier, I suspect it will only depend upon the concept of an identifier String.
Test:
{
Context context = new Context();
assertEquals("0", new Identifier("a").evaluate(context).toString()); // Evaluates to zero when not found.
assertEquals("5", new Assignment("a", new Rational("5")).evaluate(context).toString());
assertEquals("5", new Identifier("a").evaluate(context).toString());
assertEquals("7", new Assignment("a", new Rational("7")).evaluate(context).toString());
assertEquals("7", new Identifier("a").evaluate(context).toString());
}
Implementation:
class Assignment implements Statement {
private final String identifier;
private final Expression expression;
public Assignment(String identifier, Expression expression) {
this.identifier = identifier;
this.expression = expression;
}
public Rational evaluate(Context context) {
Rational rational = expression.evaluate(context);
context.add(identifier, rational);
return rational;
}
}
One Final Test
The implementation is done. However, the tests are very much in the style of unit tests. I’d like to provide one more test that demonstrates how all the components can fit together.
Test:
{
// a = 1 4/5
// b = 2 5/7
// c = a * b
// d = a + b + c
// e = a + b + c + d
// f = a * b * c * d * e
Context context = new Context();
new Assignment("a", new Rational("1 4/5")).evaluate(context);
new Assignment("b", new Rational("2 5/7")).evaluate(context);
MultiplyOp cProduct = new MultiplyOp();
cProduct.addExpression(new Identifier("a").evaluate(context));
cProduct.addExpression(new Identifier("b").evaluate(context));
new Assignment("c", cProduct).evaluate(context);
AddOp dSum = new AddOp();
dSum.addExpression(new Identifier("a").evaluate(context));
dSum.addExpression(new Identifier("b").evaluate(context));
dSum.addExpression(new Identifier("c").evaluate(context));
new Assignment("d", dSum).evaluate(context);
AddOp eSum = new AddOp();
eSum.addExpression(new Identifier("a").evaluate(context));
eSum.addExpression(new Identifier("b").evaluate(context));
eSum.addExpression(new Identifier("c").evaluate(context));
eSum.addExpression(new Identifier("d").evaluate(context));
new Assignment("e", eSum).evaluate(context);
MultiplyOp fProduct = new MultiplyOp();
fProduct.addExpression(new Identifier("a").evaluate(context));
fProduct.addExpression(new Identifier("b").evaluate(context));
fProduct.addExpression(new Identifier("c").evaluate(context));
fProduct.addExpression(new Identifier("d").evaluate(context));
fProduct.addExpression(new Identifier("e").evaluate(context));
new Assignment("f", fProduct).evaluate(context);
assertEquals("1 4/5", new Identifier("a").evaluate(context).toString());
assertEquals("2 5/7", new Identifier("b").evaluate(context).toString());
assertEquals("4 31/35", new Identifier("c").evaluate(context).toString());
assertEquals("9 2/5", new Identifier("d").evaluate(context).toString());
assertEquals("18 4/5", new Identifier("e").evaluate(context).toString());
assertEquals("4218 10488/30625", new Identifier("f").evaluate(context).toString());
}
It works, but it’s HORRIBLE. Unfortunately, this is where the Gang of Four and other Interpreter Design Pattern write ups tend to leave you. Do not fret, dear reader. I shall not abandon you. I am bound and determined to complete this DSL use case and implement it in such a way that it will be a fully functioning DSL, even if the domain is limited to Rational number evaluations.
The final implementation will be the parser, which will process the DSL and build the elements as shown above. The DSL should be easier to express intent than the raw code.
Summary
This blog presented an implementation for the operational components that will make up the Rational Expression Evalutor DSL.
The implementation proceeded smoothly, because of previous time devoted in thinking about and considering the DSL as presented in the previous Interpreter blogs. The implementation flowed naturally from the design, which flowed naturally from the grammar. The code practically writes itself. The implementation was almost anticlimactic.
References
See: Interpreter Design Pattern Introduction/References for overall references.
See: Design blog. for how the design was created.
The Complete Implementation
Here’s the entire implementation up to this point as one file. Copy and paste it into a Java environment and execute it. If you don’t have Java, try this Online Java Environment. Add more tests. Play with the implementation. Refactor some of the code. Copy and paste the code into Generative AI for analysis and comments.
A few highlights:
Rationalis a value object. Most of its complexity involves normalizing any valid rational representation to its reduced numerator and denominator.- The arithmetic operator classes are mostly fraction based arithmetic.
IdentifierandAssignmentmanage state so thatRationalvalues can be stored via a variable name an retrieved.Contextis the storage mechanism.- The classes required about 215 lines of code.
- The tests required about 170 lines of code.
- I had completely forgotten about division by zero until I had completed the implementation. I added unit tests for it, and only some worked. The code didn’t catch zero divided by zero in all cases. I didn’t retrofit the previous code with division by zero tests and updates, but I have done so in the complete listing here.
import java.util.*;
public class RationalEvaluator {
public static void main(String[] args) throws Exception {
Test.test();
}
}
interface Statement {
Rational evaluate(Context context);
}
class Context {
private final Map<String, Rational> state = new HashMap<>();
public void add(String identifier, Rational rational) {
state.put(identifier, rational);
}
public boolean containsKey(String identifier) {
return state.containsKey(identifier);
}
public Rational getRational(String identifier) {
return state.get(identifier);
}
}
interface Expression extends Statement {}
class Rational implements Expression {
private final int numerator;
private final int denominator;
public Rational(String rationalString) {
int integer = 0;
int numerator;
int denominator;
if (!rationalString.contains("/")) {
numerator = Integer.parseInt(rationalString.trim());
denominator = 1;
} else {
String[] integers = rationalString.split("/");
if (integers[0].trim().contains(" ")) {
String[] tokens = integers[0].trim().split("\\s+");
integer = Integer.parseInt(tokens[0].trim());
numerator = Integer.parseInt(tokens[1].trim());
} else {
numerator = Integer.parseInt(integers[0].trim());
}
denominator = Integer.parseInt(integers[1].trim());
numerator += integer * denominator ;
}
int divisor = denominator;
while (divisor > 1) {
if (numerator % divisor == 0 && denominator % divisor == 0) {
numerator = numerator / divisor;
denominator = denominator / divisor;
} else {
divisor--;
}
}
this.numerator = numerator;
this.denominator = denominator;
if (denominator == 0) throw new ArithmeticException();
}
public Rational evaluate(Context context) {
return this;
}
public int getNumerator() {
return numerator;
}
public int getDenominator() {
return denominator;
}
@ Override
public String toString() {
if (denominator == 1) {
return String.valueOf(numerator);
} else if (Math.abs(numerator) > denominator) {
return String.format("%d %d/%d", numerator/denominator, Math.abs(numerator%denominator), denominator);
}
return String.valueOf(numerator) + "/" + String.valueOf(denominator);
}
}
abstract class BinaryOp implements Expression {
private final Expression operand1;
private final Expression operand2;
public BinaryOp(Expression operand1, Expression operand2) {
this.operand1 = operand1;
this.operand2 = operand2;
}
public Rational evaluate(Context context) {
Rational rational1 = operand1.evaluate(context);
Rational rational2 = operand2.evaluate(context);
return operation(rational1.getNumerator(), rational1.getDenominator(), rational2.getNumerator(), rational2.getDenominator());
}
abstract protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2);
}
class SubtractOp extends BinaryOp {
public SubtractOp(Expression op1, Expression op2) {
super(op1, op2);
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * denominator2 - numerator2 * denominator1;
int denominator = denominator1 * denominator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
class DivideOp extends BinaryOp {
public DivideOp(Expression op1, Expression op2) {
super(op1, op2);
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * denominator2;
int denominator = denominator1 * numerator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
abstract class MultiOperandsOp implements Expression {
private final List<Expression> expressions = new LinkedList<>();
public void addExpression(Expression expression) {
expressions.add(expression);
}
public Rational evaluate(Context context) {
Rational accumulator = getIdentity();
for(Expression expression : expressions) {
Rational operand = expression.evaluate(context);
accumulator = operation(accumulator.getNumerator(), accumulator.getDenominator(), operand.getNumerator(), operand.getDenominator());
}
return accumulator;
}
abstract protected Rational getIdentity();
abstract protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2);
}
class AddOp extends MultiOperandsOp {
protected Rational getIdentity() {
return new Rational("0");
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * denominator2 + numerator2 * denominator1;
int denominator = denominator1 * denominator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
class MultiplyOp extends MultiOperandsOp {
protected Rational getIdentity() {
return new Rational("1");
}
protected Rational operation(int numerator1, int denominator1, int numerator2, int denominator2) {
int numerator = numerator1 * numerator2;
int denominator = denominator1 * denominator2;
return new Rational(String.format("%d/%d", numerator, denominator));
}
}
class Identifier implements Expression {
private final String identifier;
public Identifier(String identifier) {
this.identifier = identifier;
}
public Rational evaluate(Context context) {
if (!context.containsKey(identifier)) return new Rational("0");
return context.getRational(identifier);
}
}
class Assignment implements Statement {
private final String identifier;
private final Expression expression;
public Assignment(String identifier, Expression expression) {
this.identifier = identifier;
this.expression = expression;
}
public Rational evaluate(Context context) {
Rational rational = expression.evaluate(context);
context.add(identifier, rational);
return rational;
}
}
class Test {
public static void test() throws Exception {
testDesignElements();
System.out.println("TESTS PASS");
}
private static void testDesignElements() throws Exception {
assertEquals("0", new Rational("0").evaluate(null).toString());
assertEquals("1", new Rational("1 ").evaluate(null).toString());
assertEquals("-1", new Rational(" -1").evaluate(null).toString());
assertEquals("5", new Rational(" 5 ").evaluate(null).toString());
assertEquals("5", new Rational(" 5 ").evaluate(null).toString());
assertEquals("1/2", new Rational(" 1/2 ").evaluate(null).toString());
assertEquals("-1/2", new Rational(" -1/2 ").evaluate(null).toString());
assertEquals("2/3", new Rational("2 / 3").evaluate(null).toString());
try {
new Rational("1/0").evaluate(null);
throw new Exception(); // Should throw ArithmeticException and not reach here.
} catch (ArithmeticException e) {
// Expected. Division by zero.
}
try {
new Rational("0/0").evaluate(null);
throw new Exception(); // Should throw ArithmeticException and not reach here.
} catch (ArithmeticException e) {
// Expected. Division by zero.
}
assertEquals("1/2", new Rational("2/4").evaluate(null).toString());
assertEquals("1/2", new Rational("32/64").evaluate(null).toString());
assertEquals("1/4", new Rational("30 / 120").evaluate(null).toString());
assertEquals("1 2/5", new Rational("7/5").evaluate(null).toString());
assertEquals("2 1/4", new Rational("36/16").evaluate(null).toString());
assertEquals("-2 1/4", new Rational("-36/16").evaluate(null).toString());
assertEquals("5", new Rational("15 / 3").evaluate(null).toString());
assertEquals("-3", new Rational("-15 / 5").evaluate(null).toString());
assertEquals("1 5/6", new Rational("1 5/6").evaluate(null).toString());
assertEquals("2 2/3", new Rational(" 2 4 / 6 ").evaluate(null).toString());
assertEquals("4 1/2", new Rational(" 2 10 / 4 ").evaluate(null).toString());
assertEquals("5", new Rational(" 3 4 / 2 ").evaluate(null).toString());
assertEquals("1", new SubtractOp(new Rational("4"), new Rational("3")).evaluate(null).toString());
assertEquals("2 1/2", new SubtractOp(new Rational("4"), new Rational("1 1/2")).evaluate(null).toString());
assertEquals("-3", new SubtractOp(new Rational("2"), new Rational("5")).evaluate(null).toString());
assertEquals("2", new DivideOp(new Rational("4"), new Rational("2")).evaluate(null).toString());
assertEquals("3/4", new DivideOp(new Rational("3"), new Rational("4")).evaluate(null).toString());
assertEquals("1", new DivideOp(new Rational("3"), new Rational("3")).evaluate(null).toString());
assertEquals("57/110", new DivideOp(new Rational("3 4/5"), new Rational("7 1/3")).evaluate(null).toString());
try {
new DivideOp(new Rational("1"), new Rational("0")).evaluate(null);
throw new Exception(); // Should throw ArithmeticException and not reach here.
} catch (ArithmeticException e) {
// Expected. Division by zero.
}
try {
new DivideOp(new Rational("0"), new Rational("0")).evaluate(null);
throw new Exception(); // Should throw ArithmeticException and not reach here.
} catch (ArithmeticException e) {
// Expected. Division by zero.
}
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("4"));
addOp.addExpression(new Rational("3"));
assertEquals("7", addOp.evaluate(null).toString());
}
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("1/2"));
addOp.addExpression(new Rational("1/6"));
assertEquals("2/3", addOp.evaluate(null).toString());
}
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("1/2"));
addOp.addExpression(new Rational("1/6"));
addOp.addExpression(new Rational("1/6"));
assertEquals("5/6", addOp.evaluate(null).toString());
}
{
MultiOperandsOp addOp = new AddOp();
addOp.addExpression(new Rational("1 1/2"));
addOp.addExpression(new Rational("2 1/6"));
addOp.addExpression(new Rational("3 1/6"));
addOp.addExpression(new Rational("4 1/6"));
assertEquals("11", addOp.evaluate(null).toString());
}
{
MultiOperandsOp multiplyOp = new MultiplyOp();
multiplyOp.addExpression(new Rational("4"));
multiplyOp.addExpression(new Rational("3"));
assertEquals("12", multiplyOp.evaluate(null).toString());
}
{
MultiOperandsOp multiplyOp = new MultiplyOp();
multiplyOp.addExpression(new Rational("4 1/2"));
multiplyOp.addExpression(new Rational("3 1/3"));
multiplyOp.addExpression(new Rational("2 1/6"));
assertEquals("32 1/2", multiplyOp.evaluate(null).toString());
}
{
Context context = new Context();
assertEquals("0", new Identifier("a").evaluate(context).toString()); // Evaluates to zero when not found.
context.add("a", new Rational("5"));
assertEquals("5", new Identifier("a").evaluate(context).toString());
context.add("a", new Rational("7"));
assertEquals("7", new Identifier("a").evaluate(context).toString());
}
{
Context context = new Context();
assertEquals("0", new Identifier("a").evaluate(context).toString()); // Evaluates to zero when not found.
assertEquals("5", new Assignment("a", new Rational("5")).evaluate(context).toString());
assertEquals("5", new Identifier("a").evaluate(context).toString());
assertEquals("7", new Assignment("a", new Rational("7")).evaluate(context).toString());
assertEquals("7", new Identifier("a").evaluate(context).toString());
}
{
// a = 1 4/5
// b = 2 5/7
// c = a * b
// d = a + b + c
// e = a + b + c + d
// f = a * b * c * d * e
Context context = new Context();
new Assignment("a", new Rational("1 4/5")).evaluate(context);
new Assignment("b", new Rational("2 5/7")).evaluate(context);
MultiplyOp cProduct = new MultiplyOp();
cProduct.addExpression(new Identifier("a").evaluate(context));
cProduct.addExpression(new Identifier("b").evaluate(context));
new Assignment("c", cProduct).evaluate(context);
AddOp dSum = new AddOp();
dSum.addExpression(new Identifier("a").evaluate(context));
dSum.addExpression(new Identifier("b").evaluate(context));
dSum.addExpression(new Identifier("c").evaluate(context));
new Assignment("d", dSum).evaluate(context);
AddOp eSum = new AddOp();
eSum.addExpression(new Identifier("a").evaluate(context));
eSum.addExpression(new Identifier("b").evaluate(context));
eSum.addExpression(new Identifier("c").evaluate(context));
eSum.addExpression(new Identifier("d").evaluate(context));
new Assignment("e", eSum).evaluate(context);
MultiplyOp fProduct = new MultiplyOp();
fProduct.addExpression(new Identifier("a").evaluate(context));
fProduct.addExpression(new Identifier("b").evaluate(context));
fProduct.addExpression(new Identifier("c").evaluate(context));
fProduct.addExpression(new Identifier("d").evaluate(context));
fProduct.addExpression(new Identifier("e").evaluate(context));
new Assignment("f", fProduct).evaluate(context);
assertEquals("1 4/5", new Identifier("a").evaluate(context).toString());
assertEquals("2 5/7", new Identifier("b").evaluate(context).toString());
assertEquals("4 31/35", new Identifier("c").evaluate(context).toString());
assertEquals("9 2/5", new Identifier("d").evaluate(context).toString());
assertEquals("18 4/5", new Identifier("e").evaluate(context).toString());
assertEquals("4218 10488/30625", new Identifier("f").evaluate(context).toString());
}
}
private static void assertEquals(String expected, String actual) throws Exception {
if (!expected.equals(actual)) {
System.out.format("expected=%s, actual=%s\n", expected, actual);
throw new Exception();
}
}
}
